Errata
- In Figure 1.20, change one of the values from 1 to 0. (Thanks to Vladislav Boldyrev.)
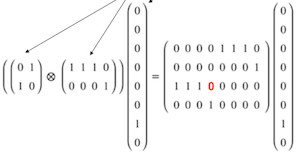 Figure 1.20
Figure 1.20
- In Figure 3.28 at the top of Page 86, the angle on the right side of the diagram is 9pi/4, not 5pi/4. (Thanks to Arend Smit for bringing this to my attention.)
- In the second bullet on Page 177, "... applying H to |1> gives us (1/sqrt(2))(|0> – |1>), also known as |–>. (Thanks again to Arend Smit.)
- The equations on Pages 210 to 212 are all correct, but they're not consistent with one another.
- The first thing on Page 108 should be \(R_Y(\frac{\pi}{\textcolor{red}{6}})\). (Thanks to Vladislav Boldyrev.)
- Several Qiskit features in the book's code have been made obsolete by the release of Qiskit 1.0.1 in February 2024. I will be posting updates for the code at https://github.com/PacktPublishing/Quantum-Computing-Algorithms. One example: Before releasing v1.0 of Qiskit, IBM had two methods (named
cnot and cx) that were identical to one another. In my book, I used cnot. When IBM released v1.0 this month, they eliminated cnot in favor of cx. There are at least two ways to fix the code in my book:
- Change every occurrence of cnot to cx.
- Run the following line at the start of each program: QuantumCircuit.cnot = QuantumCircuit.cx
(Thanks to Fujio Yamamoto.)
- In the first line of Page 263, replace the words In entry 1 with the words In entry 0. (Thanks to Fujio Yamamoto.)
- At the bottom of Page 248, replace
\( {\frac{1}{\sqrt2}}\ \vee0\rangle\ +\ {\frac{1}{\sqrt2}}\ \vee1\rangle\) to \({\frac{1}{\sqrt2}}\ \vee0\rangle\ +\ i\ {\frac{1}{\sqrt2}}\ \vee1\rangle \)
with
\( {\frac{1}{\sqrt2}}\ |0\rangle\ +\ {\frac{1}{\sqrt2}}\ |1\rangle\) to \({\frac{1}{\sqrt2}}\ |0\rangle\ +\ i\ {\frac{1}{\sqrt2}}\ |1\rangle \).
(Thanks to Fujio Yamamoto.)
- In the discussion on Pages 252 to 254, I omitted the i in exponents of e. Here are some corrections surrounding that omission:
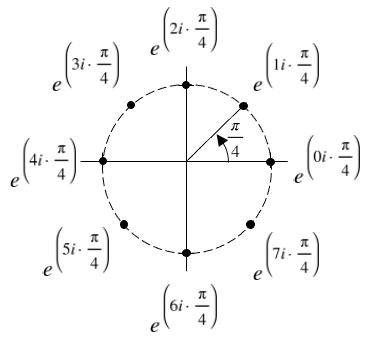 Figure 9.13
Figure 9.13
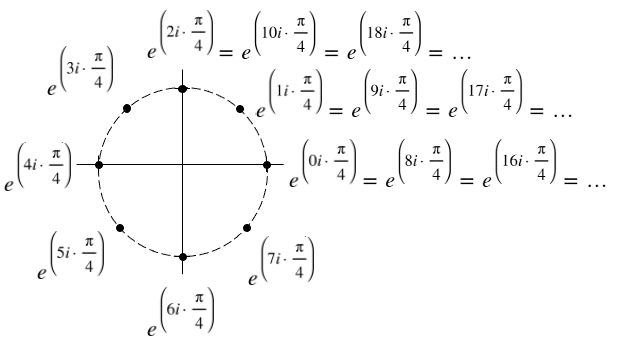 Figure 9.14
Figure 9.14
 Figure 9.15
Figure 9.15
The equation at the bottom of Page 253: \( e^{i\pi/2} \cdot e^{i\pi} = e^{i(\pi/2 + \pi)} = e^{i \cdot (3\pi/2)} \)
 Figure 9.16
Figure 9.16
(Thanks to Fujio Yamamoto.)
- In the book, Figure 9.27 is for a run that uses coprime 11. Here's a figure with the initialization numbers for coprime 7:
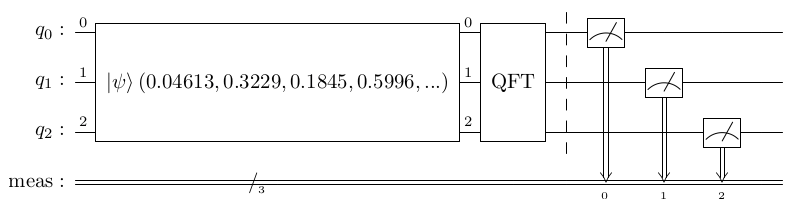 Figure 9.13
Figure 9.13
(Thanks to Fujio Yamamoto.)





